Saturday, October 23, 2010
Diodes And Rectifiers
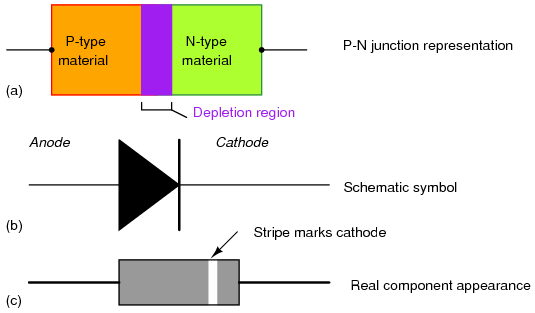
A diode is an electrical device allowing current to move through it in one direction with far greater ease than in the other. The most common kind of diode in modern circuit design is the semiconductor diode, although other diode technologies exist. Semiconductor diodes are symbolized in schematic diagrams such as Figure below. The term “diode” is customarily reserved for small signal devices, I ≤ 1 A. The term rectifier is used for power devices, I > 1 A.
Wednesday, October 13, 2010
Eigon Vectors
An eigen vector is a vector that is scaled by a linear transformation, but not moved. Think of an eigen vector as an arrow whose direction is not changed. It may stretch, or shrink, as space is transformed, but it continues to point in the same direction. Most arrows will move, as illustrated by a spinning planet, but some vectors will continue to point in the same direction, such as the north pole.
The scaling factor of an eigen vector is called its eigen value. An eigen value only makes sense in the context of an eigen vector, i.e. the arrow whose length is being changed.
In the plane, a rigid rotation of 90° has no eigen vectors, because all vectors move. However, the reflection y = -y has the x and y axes as eigen vectors. In this function, x is scaled by 1 and y by -1, the eigen values corresponding to the two eigen vectors. All other vectors move in the plane.
The y axis, in the above example, is subtle. The direction of the vector has been reversed, yet we still call it an eigen vector, because it lives in the same line as the original vector. It has been scaled by -1, pointing in the opposite direction. An eigen vector stretches, or shrinks, or reverses course, or squashes down to 0. The key is that the output vector is a constant (possibly negative) times the input vector.
These concepts are valid over a division ring, as well as a field. Multiply by K on the left to build the K vector space, and apply the transformation, as a matrix, on the right. However, the following method for deriving eigen values and vectors is based on the determinant, and requires a field.
If the eigen space is nontrivial then the determinant of Q must be 0. Expand the determinant, giving an n degree polynomial in l. (This is where we need a field, to pull all the entries to the left of l, and build a traditional polynomial.) This is called the characteristic polynomial of the matrix. The roots of this polynomial are the eigen values. There are at most n eigen values.
Substitute each root in turn and find the kernel of Q. We are looking for the set of vectors x such that x*Q = 0. Let R be the transpose of Q and solve R*x = 0, where x has become a column vector. This is a set of simultaneous equations that can be solved using gaussian elimination.
In summary, a somewhat straightforward algorithm extracts the eigen values, by solving an n degree polynomial, then derives the eigen space for each eigen value.
Some eigen values will produce multiple eigen vectors, i.e. an eigen space with more than one dimension. The identity matrix, for instance, has an eigen value of 1, and an n-dimensional eigen space to go with it. In contrast, an eigen value may have multiplicity > 1, yet there is only one eigen vector. This is illustrated by [1,1|0,1], a function that tilts the x axis counterclockwise and leaves the y axis alone. The eigen values are 1 and 1, and the eigen vector is 0,1, namely the y axis.
Select a basis b for the eigen space of l. The vectors in b are eigen vectors, with eigen value l, and every eigen vector with eigen value l is spanned by b. Conversely, an eigen vector with some other eigen value lies outside of b.
Let the first 7 vectors share a common eigen value l. If these vectors are dependent then one of them can be expressed as a linear combination of the other 6. Make this substitution and find a shorter list of dependent eigen vectors that do not all share the same eigen value. The first 6 have eigen value l, and the rest have some other eigen value. Remember, we selected the shortest list, so this is a contradiction. Therefore the eigen vectors associated with any given eigen value are independent.
Scale all the coefficients c1 through ck by a common factor s. This does not change the fact that the sum of cixi is still zero. However, other than this scaling factor, we will prove there are no other coefficients that carry the eigen vectors to 0.
If there are two independent sets of coefficients that lead to 0, scale them so the first coefficients in each set are equal, then subtract. This gives a shorter linear combination of dependent eigen vectors that yields 0. More than one vector remains, else cjxj = 0, and xj is the 0 vector. We already showed these dependent eigen vectors cannot share a common eigen value, else they would be linearly independent; thus multiple eigen values are represented. This is a shorter list of dependent eigen vectors with multiple eigen values, which is a contradiction.
If a set of coefficients carries our eigen vectors to 0, it must be a scale multiple of c1 c2 c3 … ck.
Now take the sum of cixi and multiply by M on the right. In other words, apply the linear transformation. The image of 0 ought to be 0. Yet each coefficient is effectively multiplied by the eigen value for its eigen vector, and not all eigen values are equal. In particular, not all eigen values are 0. The coefficients are not scaled equally. The new linear combination of eigen vectors is not a scale multiple of the original, and is not zero across the board. It represents a new way to combine eigen vectors to get 0. If there were two eigen values before, and one of them was zero, there is but one eigen value now. However, this means the vectors associated with that one eigen value are dependent, and we already ruled that out. Therefore we still have two or more eigen values represented. This cannot be a shorter list, so all eigen vectors are still present. In other words, all our original eigen values were nonzero. Hence a different linear combination of our eigen vectors yields 0, and that is impossible.
Therefore the eigen spaces produced by different eigen values are linearly independent.
These results, for eigen values and eigen vectors, are valid over a division ring.
The scaling factor of an eigen vector is called its eigen value. An eigen value only makes sense in the context of an eigen vector, i.e. the arrow whose length is being changed.
In the plane, a rigid rotation of 90° has no eigen vectors, because all vectors move. However, the reflection y = -y has the x and y axes as eigen vectors. In this function, x is scaled by 1 and y by -1, the eigen values corresponding to the two eigen vectors. All other vectors move in the plane.
The y axis, in the above example, is subtle. The direction of the vector has been reversed, yet we still call it an eigen vector, because it lives in the same line as the original vector. It has been scaled by -1, pointing in the opposite direction. An eigen vector stretches, or shrinks, or reverses course, or squashes down to 0. The key is that the output vector is a constant (possibly negative) times the input vector.
These concepts are valid over a division ring, as well as a field. Multiply by K on the left to build the K vector space, and apply the transformation, as a matrix, on the right. However, the following method for deriving eigen values and vectors is based on the determinant, and requires a field.
Finding Eigen Values and Vectors
Given a matrix M implementing a linear transformation, what are its eigen vectors and values? Let the vector x represent an eigen vector and let l be the eigen value. We must solve x*M = lx. Rewrite lx as x times l times the identity matrix and subtract it from both sides. The right side drops to 0, and the left side is x*M-x*l*identity. Pull x out of both factors and write x*Q = 0, where Q is M with l subtracted from the main diagonal. The eigen vector x lies in the kernel of the map implemented by Q. The entire kernel is known as the eigen space, and of course it depends on the value of l.If the eigen space is nontrivial then the determinant of Q must be 0. Expand the determinant, giving an n degree polynomial in l. (This is where we need a field, to pull all the entries to the left of l, and build a traditional polynomial.) This is called the characteristic polynomial of the matrix. The roots of this polynomial are the eigen values. There are at most n eigen values.
Substitute each root in turn and find the kernel of Q. We are looking for the set of vectors x such that x*Q = 0. Let R be the transpose of Q and solve R*x = 0, where x has become a column vector. This is a set of simultaneous equations that can be solved using gaussian elimination.
In summary, a somewhat straightforward algorithm extracts the eigen values, by solving an n degree polynomial, then derives the eigen space for each eigen value.
Some eigen values will produce multiple eigen vectors, i.e. an eigen space with more than one dimension. The identity matrix, for instance, has an eigen value of 1, and an n-dimensional eigen space to go with it. In contrast, an eigen value may have multiplicity > 1, yet there is only one eigen vector. This is illustrated by [1,1|0,1], a function that tilts the x axis counterclockwise and leaves the y axis alone. The eigen values are 1 and 1, and the eigen vector is 0,1, namely the y axis.
The Same Eigen Value
Let two eigen vectors have the same eigen value. specifically, let a linear map multiply the vectors v and w by the scaling factor l. By linearity, 3v+4w is also scaled by l. In fact every linear combination of v and w is scaled by l. When a set of vectors has a common eigen value, the entire space spanned by those vectors is an eigen space, with the same eigen value. This is not surprising, since the eigen vectors associated with l are precisely the kernel of the transfoormation defined by the matrix M with l subtracted from the main diagonal. This kernel is a vector space, and so is the eigen space of l.Select a basis b for the eigen space of l. The vectors in b are eigen vectors, with eigen value l, and every eigen vector with eigen value l is spanned by b. Conversely, an eigen vector with some other eigen value lies outside of b.
Different Eigen Values
Different eigen values always lead to independent eigen spaces. Suppose we have the shortest counterexample. Thus c1x1 + c2x2 + … + ckxk = 0. Here x1 through xk are the eigen vectors, and c1 through ck are the coefficients that prove the vectors form a dependent set. Furthermore, the vectors represent at least two different eigen values.Let the first 7 vectors share a common eigen value l. If these vectors are dependent then one of them can be expressed as a linear combination of the other 6. Make this substitution and find a shorter list of dependent eigen vectors that do not all share the same eigen value. The first 6 have eigen value l, and the rest have some other eigen value. Remember, we selected the shortest list, so this is a contradiction. Therefore the eigen vectors associated with any given eigen value are independent.
Scale all the coefficients c1 through ck by a common factor s. This does not change the fact that the sum of cixi is still zero. However, other than this scaling factor, we will prove there are no other coefficients that carry the eigen vectors to 0.
If there are two independent sets of coefficients that lead to 0, scale them so the first coefficients in each set are equal, then subtract. This gives a shorter linear combination of dependent eigen vectors that yields 0. More than one vector remains, else cjxj = 0, and xj is the 0 vector. We already showed these dependent eigen vectors cannot share a common eigen value, else they would be linearly independent; thus multiple eigen values are represented. This is a shorter list of dependent eigen vectors with multiple eigen values, which is a contradiction.
If a set of coefficients carries our eigen vectors to 0, it must be a scale multiple of c1 c2 c3 … ck.
Now take the sum of cixi and multiply by M on the right. In other words, apply the linear transformation. The image of 0 ought to be 0. Yet each coefficient is effectively multiplied by the eigen value for its eigen vector, and not all eigen values are equal. In particular, not all eigen values are 0. The coefficients are not scaled equally. The new linear combination of eigen vectors is not a scale multiple of the original, and is not zero across the board. It represents a new way to combine eigen vectors to get 0. If there were two eigen values before, and one of them was zero, there is but one eigen value now. However, this means the vectors associated with that one eigen value are dependent, and we already ruled that out. Therefore we still have two or more eigen values represented. This cannot be a shorter list, so all eigen vectors are still present. In other words, all our original eigen values were nonzero. Hence a different linear combination of our eigen vectors yields 0, and that is impossible.
Therefore the eigen spaces produced by different eigen values are linearly independent.
These results, for eigen values and eigen vectors, are valid over a division ring.
Axis of Rotation
Here is a simple application of eigen vectors. A rigid rotation in 3 space always has an axis of rotation. Let M implement the rotation. The determinant of M, with l subtracted from its main diagonal, gives a cubic polynomial in l, and every cubic has at least one real root. Since lengths are preserved by a rotation, l is ±1. If l is -1 we have a reflection. So l = 1, and the space rotates through some angle θ about the eigen vector. That's why every planet, every star, has an axis of rotation.Wednesday, October 6, 2010
Lasers
A laser is constructed from three principal parts:
The pump source is the part that provides energy to the laser system. Examples of pump sources include electrical discharges, flashlamps, arc lamps, light from another laser, chemical reactions and even explosive devices. The type of pump source used principally depends on the gain medium, and this also determines how the energy is transmitted to the medium. A helium-neon (HeNe) laser uses an electrical discharge in the helium-neon gas mixture, a Nd:YAG laser uses either light focused from a xenon flash lamp or diode lasers, and excimer lasers use a chemical reaction.laser is not only light source
The gain medium is the major determining factor of the wavelength of operation, and other properties, of the laser.Gain media in different materials have linear spectra or wide spectra.Gain media with wide spectra allow tune frequency of laser.First wide tunable crystal laser with tunabulity more octave represent on photo 3 http://spie.org/x39922.xml . There are hundreds if thousands of different gain media in which laser operation has been achieved (see list of laser types for a list of the most important ones). The gain medium is excited by the pump source to produce a population inversion, and it is in the gain medium that spontaneous and stimulated emission of photons takes place, leading to the phenomenon of optical gain, or amplification.
Examples of different gain media include:
The optical resonator, or optical cavity, in its simplest form is two parallel mirrors placed around the gain medium which provide feedback of the light. The mirrors are given optical coatings which determine their reflective properties. Typically one will be a high reflector, and the other will be a partial reflector. The latter is called the output coupler, because it allows some of the light to leave the cavity to produce the laser's output beam.
Light from the medium, produced by spontaneous emission, is reflected by the mirrors back into the medium, where it may be amplified by stimulated emission. The light may reflect from the mirrors and thus pass through the gain medium many hundreds of times before exiting the cavity. In more complex lasers, configurations with four or more mirrors forming the cavity are used. The design and alignment of the mirrors with respect to the medium is crucial to determining the exact operating wavelength and other attributes of the laser system.
Other optical devices, such as spinning mirrors, modulators, filters, and absorbers, may be placed within the optical resonator to produce a variety of effects on the laser output, such as altering the wavelength of operation or the production of pulses of laser light.
Some lasers do not use an optical cavity, but instead rely on very high optical gain to produce significant amplified spontaneous emission (ASE) without needing feedback of the light back into the gain medium. Such lasers are said to be superluminescent, and emit light with low coherence but high bandwidth. Since they do not use optical feedback, these devices are often not categorized as lasers.
Q-switching, sometimes known as giant pulse formation, is a technique by which a laser can be made to produce a pulsed output beam. The technique allows the production of light pulses with extremely high (gigawatt) peak power, much higher than would be produced by the same laser if it were operating in a continuous wave (constant output) mode. Compared to modelocking, another technique for pulse generation with lasers, Q-switching leads to much lower pulse repetition rates, much higher pulse energies, and much longer pulse durations. Both techniques are sometimes applied at once.
Initially the laser medium is pumped while the Q-switch is set to prevent feedback of light into the gain medium (producing an optical resonator with low Q). This produces a population inversion, but laser operation cannot yet occur since there is no feedback from the resonator. Since the rate of stimulated emission is dependent on the amount of light entering the medium, the amount of energy stored in the gain medium increases as the medium is pumped. Due to losses from spontaneous emission and other processes, after a certain time the stored energy will reach some maximum level; the medium is said to be gain saturated. At this point, the Q-switch device is quickly changed from low to high Q, allowing feedback and the process of optical amplification by stimulated emission to begin. Because of the large amount of energy already stored in the gain medium, the intensity of light in the laser resonator builds up very quickly; this also causes the energy stored in the medium to be depleted almost as quickly. The net result is a short pulse of light output from the laser, known as a giant pulse, which may have a very high peak intensity.
- An energy source (usually referred to as the pump or pump source),
- A gain medium or laser medium, and
- Two or more mirrors that form an optical resonator.
Pump source
The pump source is the part that provides energy to the laser system. Examples of pump sources include electrical discharges, flashlamps, arc lamps, light from another laser, chemical reactions and even explosive devices. The type of pump source used principally depends on the gain medium, and this also determines how the energy is transmitted to the medium. A helium-neon (HeNe) laser uses an electrical discharge in the helium-neon gas mixture, a Nd:YAG laser uses either light focused from a xenon flash lamp or diode lasers, and excimer lasers use a chemical reaction.laser is not only light source
Gain medium / Laser medium
The gain medium is the major determining factor of the wavelength of operation, and other properties, of the laser.Gain media in different materials have linear spectra or wide spectra.Gain media with wide spectra allow tune frequency of laser.First wide tunable crystal laser with tunabulity more octave represent on photo 3 http://spie.org/x39922.xml . There are hundreds if thousands of different gain media in which laser operation has been achieved (see list of laser types for a list of the most important ones). The gain medium is excited by the pump source to produce a population inversion, and it is in the gain medium that spontaneous and stimulated emission of photons takes place, leading to the phenomenon of optical gain, or amplification.
Examples of different gain media include:
- Liquids, such as dye lasers. These are usually organic chemical solvents, such as methanol, ethanol or ethylene glycol, to which are added chemical dyes such as coumarin, rhodamine and fluorescein. The exact chemical configuration of the dye molecules determines the operation wavelength of the dye laser.
- Gases, such as carbon dioxide, argon, krypton and mixtures such as helium-neon. These lasers are often pumped by electrical discharge.
- Solids, such as crystals and glasses. The solid host materials are usually doped with an impurity such as chromium, neodymium, erbium or titanium ions. Typical hosts include YAG (yttrium aluminium garnet), YLF (yttrium lithium fluoride), sapphire (aluminium oxide) and various glasses. Examples of solid-state laser media include Nd:YAG, Ti:sapphire, Cr:sapphire (usually known as ruby), Cr:LiSAF (chromium-doped lithium strontium aluminium fluoride), Er:YLF, Nd:glass, and Er:glass. Solid-state lasers are usually pumped by flashlamps or light from another laser.
- Semiconductors, a type of solid, crystal with uniform dopant distrubution or material with differing dopant levels in which the movement of electrons can cause laser action. Semiconductor lasers are typically very small, and can be pumped with a simple electric current, enabling them to be used in consumer devices such as compact disc players. See laser diode.
Optical resonator
The optical resonator, or optical cavity, in its simplest form is two parallel mirrors placed around the gain medium which provide feedback of the light. The mirrors are given optical coatings which determine their reflective properties. Typically one will be a high reflector, and the other will be a partial reflector. The latter is called the output coupler, because it allows some of the light to leave the cavity to produce the laser's output beam.
Light from the medium, produced by spontaneous emission, is reflected by the mirrors back into the medium, where it may be amplified by stimulated emission. The light may reflect from the mirrors and thus pass through the gain medium many hundreds of times before exiting the cavity. In more complex lasers, configurations with four or more mirrors forming the cavity are used. The design and alignment of the mirrors with respect to the medium is crucial to determining the exact operating wavelength and other attributes of the laser system.
Other optical devices, such as spinning mirrors, modulators, filters, and absorbers, may be placed within the optical resonator to produce a variety of effects on the laser output, such as altering the wavelength of operation or the production of pulses of laser light.
Some lasers do not use an optical cavity, but instead rely on very high optical gain to produce significant amplified spontaneous emission (ASE) without needing feedback of the light back into the gain medium. Such lasers are said to be superluminescent, and emit light with low coherence but high bandwidth. Since they do not use optical feedback, these devices are often not categorized as lasers.
Q-SWITCHING
Q-switching, sometimes known as giant pulse formation, is a technique by which a laser can be made to produce a pulsed output beam. The technique allows the production of light pulses with extremely high (gigawatt) peak power, much higher than would be produced by the same laser if it were operating in a continuous wave (constant output) mode. Compared to modelocking, another technique for pulse generation with lasers, Q-switching leads to much lower pulse repetition rates, much higher pulse energies, and much longer pulse durations. Both techniques are sometimes applied at once.
Principle of Q-switching:
Q-switching is achieved by putting some type of variable attenuator inside the laser's optical resonator. When the attenuator is functioning, light which leaves the gain medium does not return, and lasing cannot begin. This attenuation inside the cavity corresponds to a decrease in the Q factor or quality factor of the optical resonator. A high Q factor corresponds to low resonator losses per roundtrip, and vice versa. The variable attenuator is commonly called a "Q-switch", when used for this purpose.Initially the laser medium is pumped while the Q-switch is set to prevent feedback of light into the gain medium (producing an optical resonator with low Q). This produces a population inversion, but laser operation cannot yet occur since there is no feedback from the resonator. Since the rate of stimulated emission is dependent on the amount of light entering the medium, the amount of energy stored in the gain medium increases as the medium is pumped. Due to losses from spontaneous emission and other processes, after a certain time the stored energy will reach some maximum level; the medium is said to be gain saturated. At this point, the Q-switch device is quickly changed from low to high Q, allowing feedback and the process of optical amplification by stimulated emission to begin. Because of the large amount of energy already stored in the gain medium, the intensity of light in the laser resonator builds up very quickly; this also causes the energy stored in the medium to be depleted almost as quickly. The net result is a short pulse of light output from the laser, known as a giant pulse, which may have a very high peak intensity.
Types of lasers
 |
| Energy Diagram for He Ne laser |
 |
| Ruby laser diagram |
IC Engines: Basics
The internal combustion engine is a heat engine in which the burning of a fuel occurs in a confined space called a combustion chamber. This exothermic reaction of a fuel with an oxidizer creates gases of high temperature and pressure, which are permitted to expand. The defining feature of an internal combustion engine is that useful work is performed by the expanding hot gases acting directly to cause movement, for example by acting on pistons, rotors, or even by pressing on and moving the entire engine itself.
I hope these pictures and articles will be very usefull for those who are studying the concepts of basic Mechanical Engineering
I hope these pictures and articles will be very usefull for those who are studying the concepts of basic Mechanical Engineering
 |
| 4 stroke engine |
Subscribe to:
Comments (Atom)